介绍
AVL 树(Adelson-Velskii-Landis Tree)是平衡二叉搜索树的一种,可以看作是有附加条件的二叉搜索树,用以保证不会出现如下极端情况。
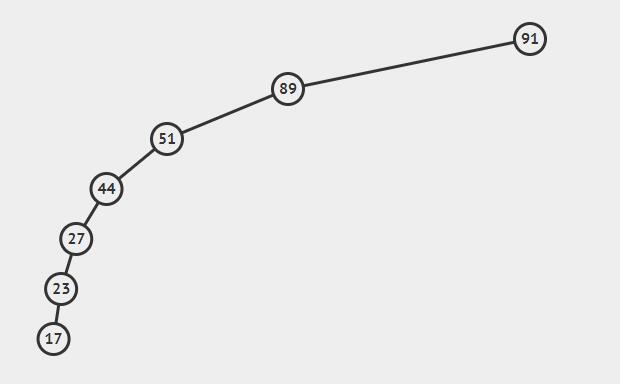
之所以这么做是为了保证整棵树深度在 \(O(logN)\) ,从而使得插入和删除结点时不会因极端情况导致花费过长时间。AVL 树的要求是 任何节点的左右子树高度相差不超过 1,如下图所示。
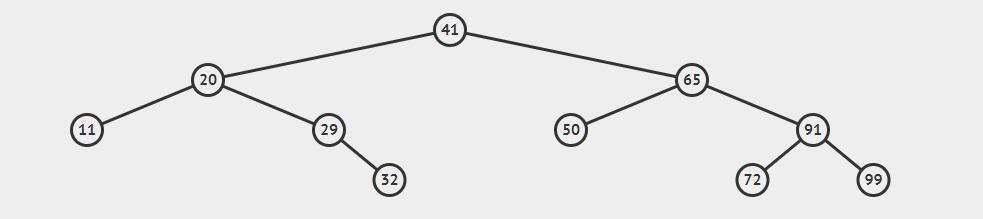
仔细观察普通的二叉搜索树可以发现只有在插入操作时会影响到树的平衡,所以需要稍加修正以恢复性质,这一过程称为旋转(rotation)。
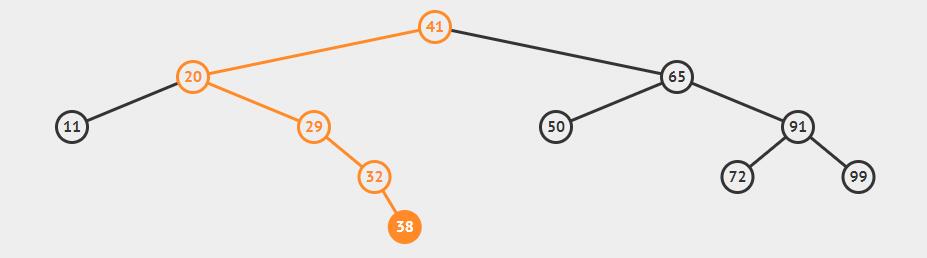
从上图可以看出,在插入38后,以20为根的子树右侧高度比左侧高2,不再满足AVL树平衡条件,所以我们需要将其右子树高度调整为2。
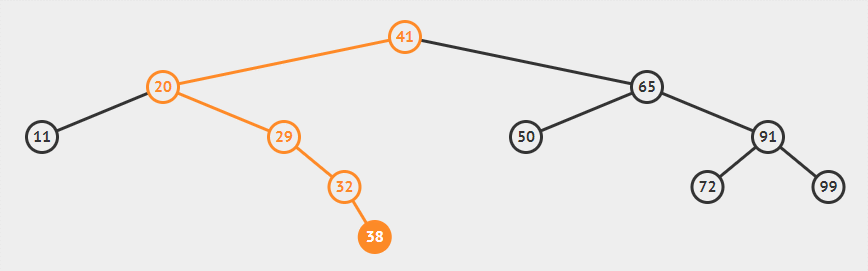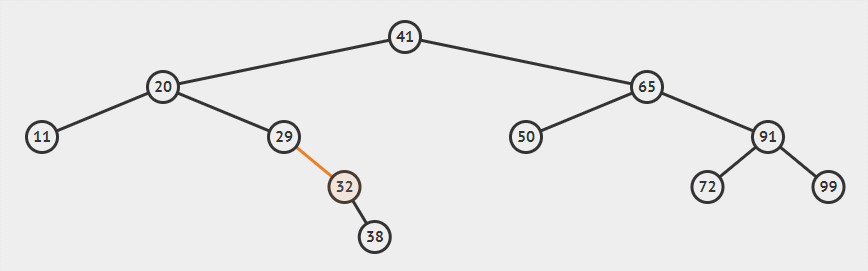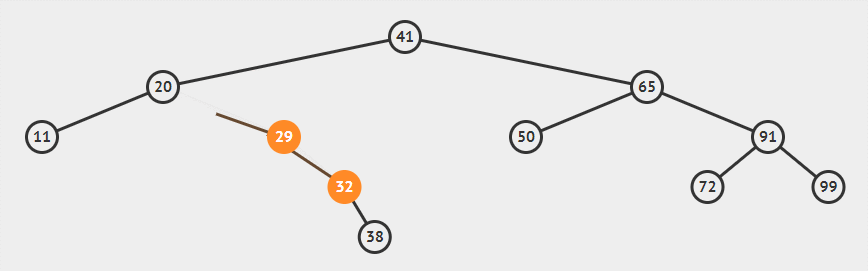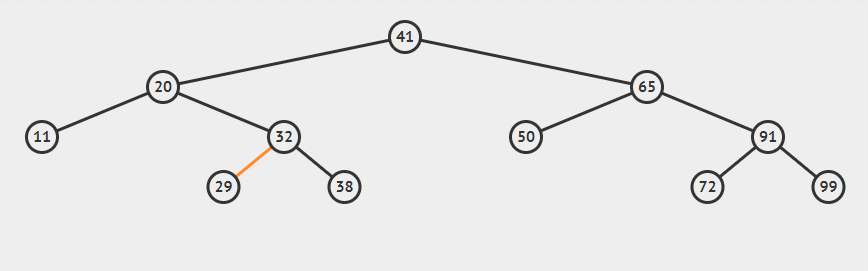
上图演示了如何恢复平衡。其中20是产生不平衡的树的根节点,插入点位于其右子节点的右侧,所以称之为“右右”旋转。将发生不平衡的根节点称为 X,总共有发生如下四种情况:
- 对 X 的左子节点的左子树进行一次插入 —— 左左
- 对 X 的左子节点的右子树进行一次插入 —— 左右
- 对 X 的右子节点的左子树进行一次插入 —— 右左
- 对 X 的右子节点的右子树进行一次插入 —— 右右
其中,1与4、2与3相互对称,前者插入点均在外侧,可通过单旋转完成,后者插入点在内侧,需要进行双旋转。
单旋转
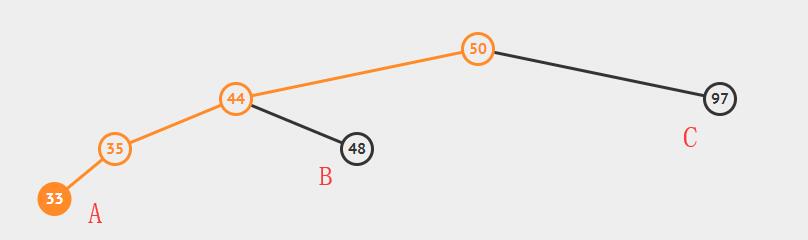
插入33后,A子树增长了一层,从而比C子树深度多2,而B子树不可能与A同一层,所以为了使得树恢复平衡,需要将A子树上移,C子树下移,从而产生一棵等价的树。
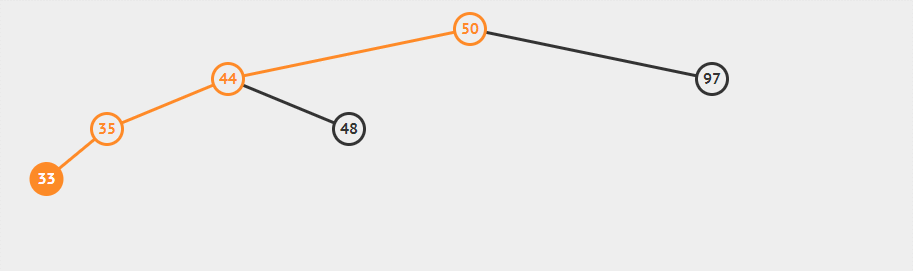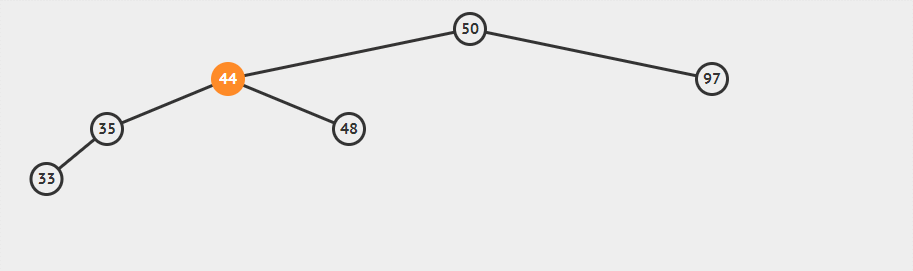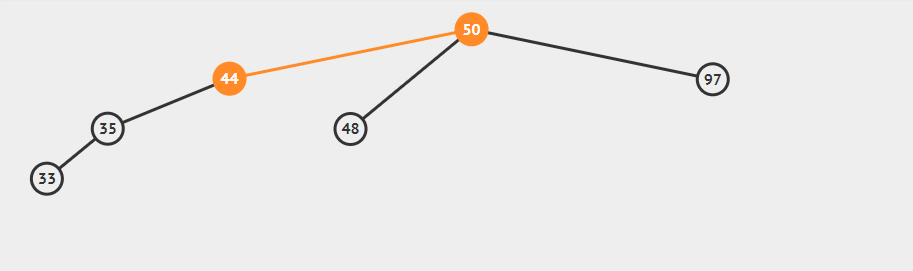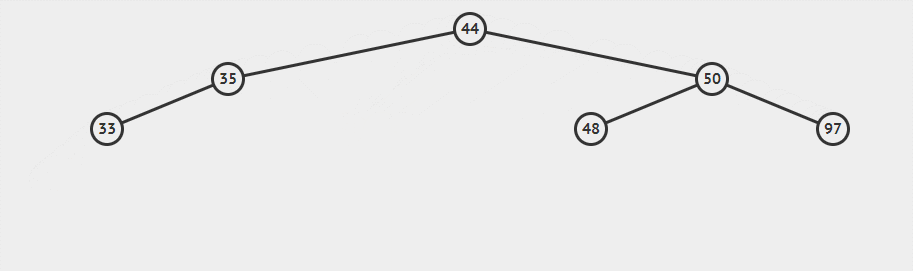
这一过程可以看作将44向上拉,50便滑落至右侧。需要注意的是48这一结点,即B子树,其中所有结点应当大于44小于50,根据二叉平衡树的性质,需要将其父节点调整至50的左侧。
双旋转
在之前一种情况中,我们并没有改变B子树的深度,因为它并不影响到平衡成立,然而如下图当它是破坏平衡条件的时候,单旋转便不再有用,因为无论以40或50作为根节点都无法满足条件。
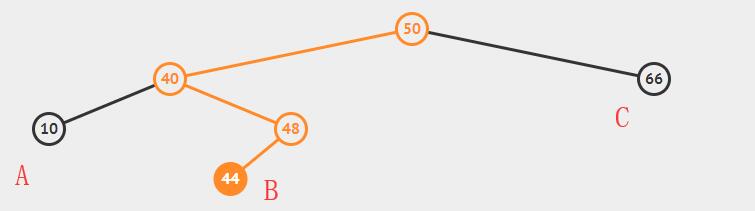
这种情况下,只有48能作为新的根节点,这样四棵子树位置便是确定的。A与C子树位置保持不变,B子树小于48大于40,所以成为40新的右子树,原48的右子树小于50大于48,所以成为50的新左子树。
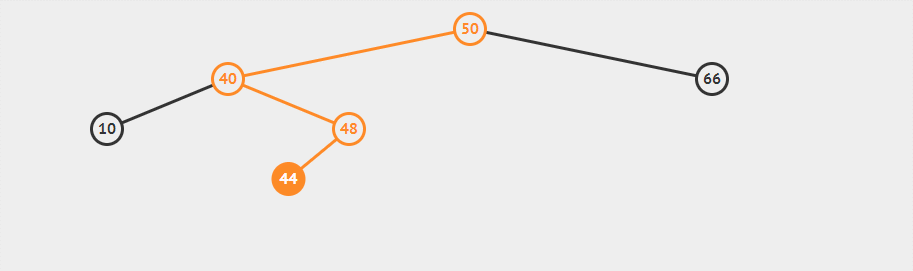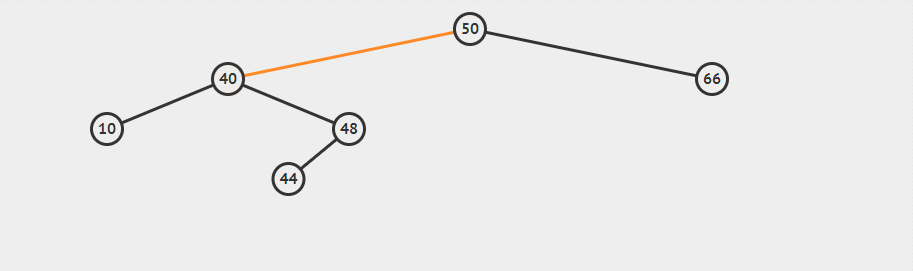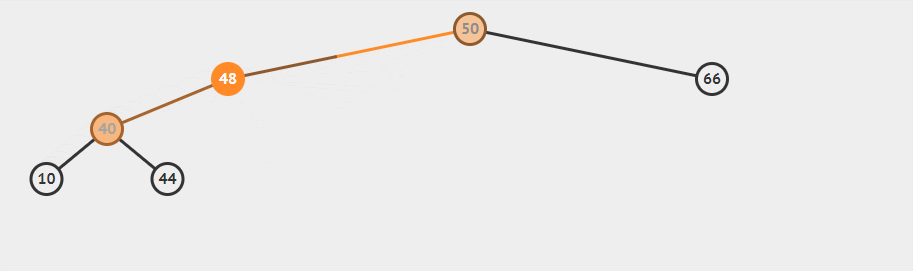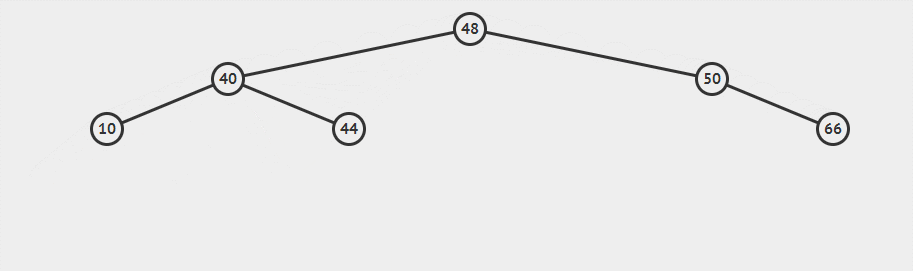
两次单旋转分别使得48上移,同时注意其子树移动。
以上所有操作只需要对指针稍作调整便可以满足AVL树平衡条件。