在分析算法性能的时候,通常有空间复杂度和时间复杂度两个维度,前者考虑的是对于存储空间的占用,后者考虑的是算法完成所需要的时间,在分析时候有许多记号用于不同需求时的表示。
通常来说复杂度与输入的规模有关,下文中 n 均表示输入规模。
Θ 记号
\(\Theta (g(n))\) 用来表示一类函数 \(f(n)\) ,存在 \(c_1、c_2\) 和 \(n_0\),使得对于所有 \(n \ge n_0\),都有 \(0 \le c_1 g(n) \le f(n) \le c_2 g(n)\)。
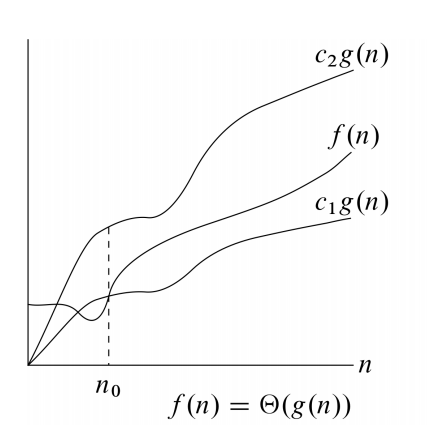
换句话说就是当 n 足够大以后,如上图所示,\(f(n)\) 会被始终夹在两者之间,那么就认为 \(f(n) \in \Theta (g(n))\),但通常来说用等号替代属于符号,即 \(f(n) = \Theta (g(n))\)。
最为常见的是关于 n 的时间复杂度是多项式,在使用 \(\Theta\)时通常我们可以仅保留最高阶项,并舍弃常数。例如 \(4n^3+20n^2+100\) 可以记作 \(\Theta (n^3)\)。
之所以可以这么做是因为我们往往考虑的是当 n 极大时候的性能,当 n 足够大时,低阶项无论前面常数多大也是无足轻重的,而最高阶系数仅对于定义中 \(c_1\) 和 \(c_2\) 选取有关,而不影响到 \(g(n)\)。所以一般来说都有
\[\forall \ p(n) = \sum_{i=0}^{d} a_i n^i ,\ 都有 \ p(n) = \Theta (n^d)\]其中 \(a_i\) 都是常量且 \(a_d > 0\)。对于 0 阶多项式,即常数,一般记作 \(\Theta (1)\)。
值得一提的是,在分析时间复杂度时候,n 较小的情况一般不考虑,因为绝大多数情况下考虑的是输入规模很大时候的性能,本文中的记号也都是设计用来考虑规模很大时候的性能。但在有些场景中 n 有限,此时低阶项系数可能仍发挥着不可忽视的作用,此时仅使用 \(\Theta\) 可能并不能得到最优的方法。
O 记号
\(O(g(n))\) 表示一类函数 \(f(n)\),存在 \(c\) 和 \(n_0\),使得对于所有 \(n \ge n_0\),都有 \(0 \le f(n) \le c g(n)\)。一般读作“大 O”或者“Big-Oh”。
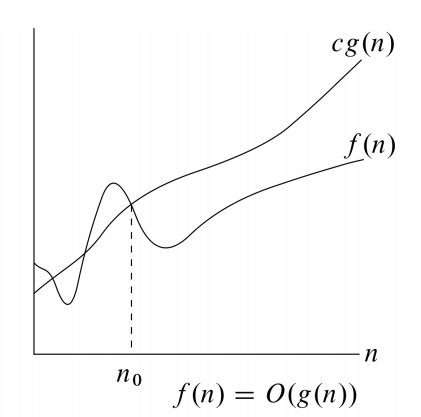
相比于 \(\Theta\) 渐进的给出了上界和下届,\(O\) 只考虑渐近上届。因此类似于 \(n = O(n^2)\) 也是合法的,因为很显然当 n 很大时,一次函数必定始终小于一个二次函数。
尽管可能会有那么一些不准确,但是可以用它来仅仅通过检查代码结构来描述运行时间。比如一个双重嵌套的循环,两个循环都与 n 有关,循环内是常数时间即可完成的,那么就可以得出一个 \(O(n^2)\) 的上界。当然具体运行的时间依赖于具体输入,但至少利用 \(O\) 可以得到无论任何输入的一个最坏上界。
Ω 记号
\(\Omega (g(n))\) 表示一类函数 \(f(n)\),存在 \(c\) 和 \(n_0\),使得对于所有 \(n \ge n_0\),都有 \(0 \ge c g(n) \ge f(n)\)。
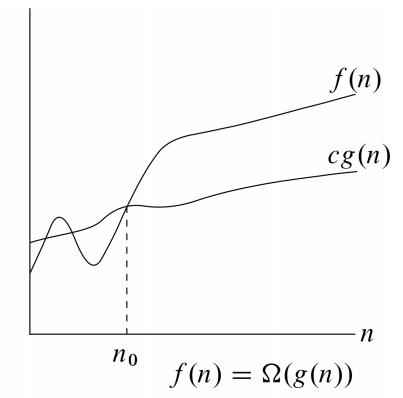
与 \(O\) 记号类似,\(\Omega\) 提供了一个渐进下界。
o 和 ω 记号
\(O\) 记号中给出的上界可能是渐进紧确的,也可能不是。例如 \(2n^2 = O(n^2)\) 就是渐进紧确的,而 \(2n =O(n^2)\)就不是。\(o\) 记号就是用来表示一个非渐进紧确的上界。相对于\(O\)的定义,要求对于任意 \(c > 0\) 都存在 \(n_0 > 0\) 有 \(0 \le f(n) < c g(n)\)。
所以 \(2n = o(n^2)\),而 \(2n^2 \ne o(n^2)\)。对于 \(f(n)=o(g(n))\),当 n 趋于无穷时,\(f(n)\) 相对于 \(g(n)\)就会显得微不足道,即 \(\lim_{n\to \infty} \frac{f(n)}{g(n)} = 0\)。
\(\omega\) 与 \(\Omega\) 间区别与 \(O\) 和 \(o\) 间关系相同,用来表示非渐进紧确的下界。例如 \(2n^2 = \omega (n)\),而 \(2n \ne \omega (n^2)\)。对于 \(f(n)=o(g(n))\),当 n 趋于无穷时,则有 \(\lim_{n\to \infty} \frac{f(n)}{g(n)} = \infty\)。
关系
定理
- 对于任意两个函数 \(f(n)\) 和 \(g(n)\),有 \(f(n)=\Theta (g(n))\),当且仅当 \(f(n) = O(g(n))\) 且 \(f(n) = \Omega (g(n))\)。
传递性
- 若 \(f(n) = \Theta (g(n))\) 且 \(g(n) = \Theta (h(n))\),则有 \(f(n) = \Theta (h(n))\)
- 若 \(f(n) = O (g(n))\) 且 \(g(n) = O (h(n))\),则有 \(f(n) = O (h(n))\)
- 若 \(f(n) = \Omega (g(n))\) 且 \(g(n) = \Omega (h(n))\),则有 \(f(n) = \Omega (h(n))\)
- 若 \(f(n) = o (g(n))\) 且 \(g(n) = o (h(n))\),则有 \(f(n) = o (h(n))\)
- 若 \(f(n) = \omega (g(n))\) 且 \(g(n) = \omega (h(n))\),则有 \(f(n) = \omega (h(n))\)
自反性
- \(f(n)\) = \(\Theta (f(n))\)
- \(f(n)\) = \(O (f(n))\)
- \(f(n)\) = \(\Omega (f(n))\)
对称性
- \(f(n) = \Theta (g(n))\) 当且仅当 \(g(n) = \Theta (f(n))\)
转置对称性
- \(f(n) = O (g(n))\) 当且仅当 \(g(n) = \Omega (f(n))\)
- \(f(n) = o (g(n))\) 当且仅当 \(g(n) = \omega (f(n))\)
运算法则
- \(O(f) + O(g)\) = \(O(max(f,g))\) = \(O(f+g)\)
- \(O(f)O(g)\) = \(O(fg)\)
- \(O(cf(n))\) = \(O(f(n))\)
总结
五种符号分别用于几种不同的比较情况,\(O(f)\) 记号代表了上确界小于等于 \(f\) 的函数集合,\(\Omega (f)\) 代表了下确界大于等于 \(f\) 的函数集合,\(\Theta (n)\) 则代表了上下确界均为 \(f\) 的函数集合。而 \(o\) 和 \(\omega\) 则与大写的类似,但不再允许相等。因此可以有如下的类比。
| 记号 | 类似 |
|---|---|
| \(f(n) = \Theta (g(n))\) | \(a = b\) |
| \(f(n) = O (g(n))\) | \(a \le b\) |
| \(f(n) = \Omega (g(n))\) | \(a \ge b\) |
| \(f(n) = o (g(n))\) | \(a < b\) |
| \(f(n) = \omega (g(n))\) | \(a > b\) |